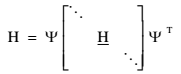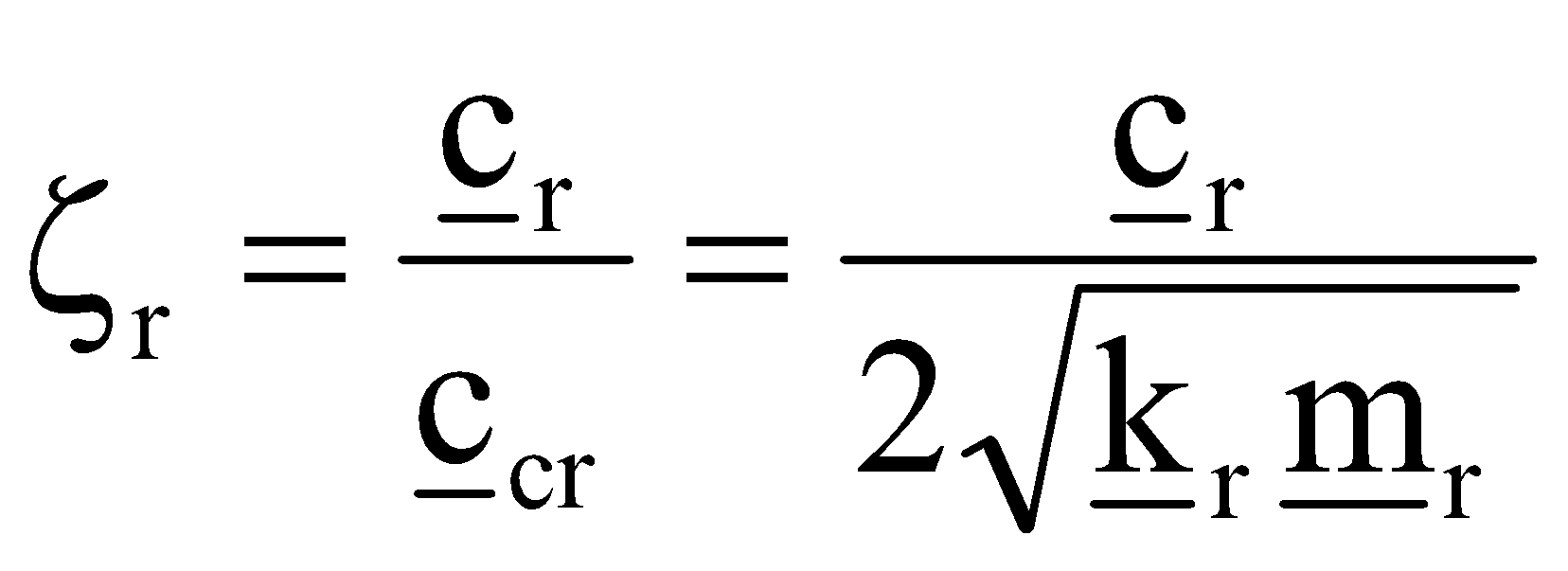Dynamic Defect Detection – Part I Theory
Part I – Theory
Neil Coleman, President/CEO
Robert E. Coleman, Senior Applications Specialist
Signalysis, Inc.
Wide-ranging measurement methods are applied on the assembly lines of production plants across the country. The ever-rising bar of quality demands rejection of defective products at an assurance level not imagined in years past. The future of defect detection perhaps lies in the identification of assembly line units that are not yet defective, but which could nonetheless be expected to fail prematurely in the hands of the consumer.
A production test activity once dominated by mechanically operated micrometers now is characterized by computer controlled measurement devices and data acquisition and analysis systems. Yet, many production plants have not taken advantage of newly developed methods of dynamic measurement and signal processing.
This article suggests dynamic testing as a means of detecting not only on-the-line defects, but also the potential for premature failure after delivery to the customer.
The Dynamic Defect Detection Concept
It has been found that a large variety of products possess intrinsic dynamic characteristics that provide a signature of the state of their health. A product’s signature, or fingerprint, is revealed through mechanical vibration that is measured as part of the detection process.
The key feature of the dynamic defect detection process is the integration of fast, continuous response measurement devices, high-speed data acquisition, advanced time and frequency domain signal processing, data analysis, and production line disposition and control. Statistical analysis methods are combined with techniques of time and frequency domain finger printing.
The focus here is on the use of mechanical vibration measurements for rating product health.
Single-Degree-Of-Freedom Vibration Theory
Most products, from small to large – from components, computers, TVs, appliances, motors, and equipment to vehicles, aircraft, bridges and buildings – are rich in vibration characteristics that can indicate their state of health. The reason is that, in a mechanical dynamical sense, these products are all composed of quite a large number of masses, springs, and dampers. And every combination of a mass, spring and damper has an associated resonance frequency and a mathematical characteristic we call the SDOF FRF (single-degree-of-freedom frequency response function). The combination of many masses, springs, and dampers within a product results in many resonance frequencies, along with the superposition of their FRFs. The FRF resulting from this superposition manifests a myriad of markers useful for assessing product integrity.
The FRF is fundamental to the understanding of the richness of intrinsic vibration characteristics of a product. It is a mathematical function derived from measurements of an applied dynamic force along with the vibratory response motion, which could be displacement, velocity or acceleration.
The FRF concept can be understood in association with the simple mass, spring, and damper in Figure 1. A vibratory force, f(t), is applied to the mass, inducing response vibration displacement, x(t). The applied force is typically a random time function having a continuous spectrum over the frequency range of interest. The FRF results from the solution of the differential equation of motion for the SDOF system.

A) B)
Figure 1. A vibratory force is applied to a simple mass, spring, and damper system (A). The differential equation of motion is developed from the free-body diagram (B). This equation describes the vibration displacement response of the system.
This equation is obtained by setting the sum of forces acting on the mass equal to the product of mass times acceleration (Newton’s Second Law):
(1)![]()
where:
f(t) = time-dependent force (lb.)
x = time dependent displacement (in.)
m = system mass (lbm)
k = spring stiffness (lb./in.)
c = viscous damping (lb./in./s).
The FRF is a frequency domain function, and we derive it by first taking the Fourier transform of Equation (1). One of the benefits of transforming the time-dependent differential equation is that a fairly easy algebraic equation results, owing to the simple relationship between displacement, velocity, and acceleration in the frequency domain. These relationships lead to an equation that includes only the displacement and force as functions of frequency. Letting F(ω) represent the Fourier Transform of force and X(ω) represent the transform of displacement:
![]() (2)
(2)
The circular frequency, ω, is used here (radians/s). The damping term is imaginary, due to the 90-degree phase shift of velocity with respect to displacement for sinusoidal motion. Now the FRF is obtained by solving for the ratio of the displacement Fourier transform to the force Fourier transform. The FRF is usually indicated by the notation, h(ω).
![]() (3)
(3)
After rationalizing the denominator and defining some key parameters in a more popular form, Equation (3) is written:
(4)![]()
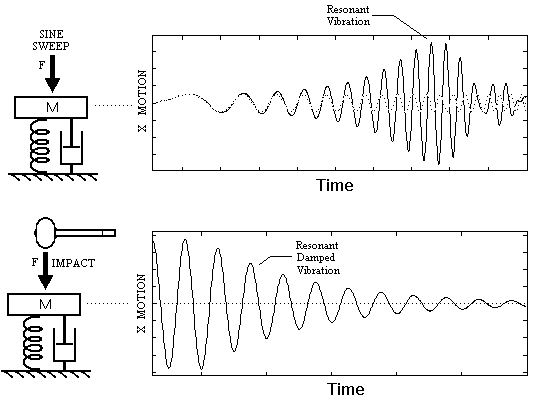
This form of the FRF allows one to recognize the real and imaginary parts separately. The new parameters introduced in Equation (4) are the frequency ratio, β = ω/ωr, and the damping factor, ζ. These parameters become clearer upon considering two different ways of inducing vibration on the SDOF system. Figure 2 illustrates the vibration behavior under forced sinusoidal vibration with a continuously increasing frequency compared to vibration resulting from a sudden impact.
The upper diagram of Figure 2 depicts a process in which a computer-controlled electrodynamic shaker impresses a vibration force that slowly sweeps up from a low frequency to a high frequency. The mass and spring respond with amplified vibration as the shaker sweeps into that special frequency range of system resonance. The level of vibration response when forced at the resonance frequency, ωr, depends on the amount of damping as quantified by the damping constant, c. The damping factor, ζ, is the ratio of actual damping, c, to the damping value known as critical damping, cc. A system with ζ greater than or equal to 1.0 will not vibrate freely. Typical product values of ζ range from .01 to .05, except for products specifically designed with high damping, ζ > 0.1, to inhibit vibration.
The lower diagram of Figure 2 reflects that same resonant property of the spring-mass system. The mass and spring are shocked into vibration at the system resonance frequency. The vibration dies away with time at a decay rate dependent on the damping constant, c.
Figure 2. Vibration response of a SDOF system to two different excitation processes. The upper diagram shows response to an applied sine sweep forcing function, and the lower diagram shows response to a hammer impact force.
Actually, either of the two displacement-time functions plotted in Figure 2 could be derived from the differential Equation (1). Just enter either the sine sweep forcing function or the hammer impact force for f(t) in Equation (1) and solve for the displacement response. But, an efficient use of the data from either of the vibration processes would be to Fourier Transform force and displacement measurements and compute the FRF. This result is sketched in Figure 3.
Figure 3. The FRF (frequency response function) plot for the SDOF of Figure 1. The FRF could be computed from the Fourier Transform ratio, X(ω)/F(ω), using data from either of the Figure 2 vibration processes. The FRF peaks at the system resonance frequency, ωr.
The FRF of Figure 3 directly reflects the sine sweep process. The system response is fairly constant throughout the low frequency range and rises to a peak at the resonance frequency, ωr. The resonance frequency can be shown to depend on the system mass and stiffness:
(5)
Multiple Degree Of Freedom Systems
There is a reason for this extensive excursion into SDOF vibration theory. It is because the most complicated structure, having a large number of masses and springs and resonance frequencies can be understood as a superposition of simple SDOF systems. Such a complicated system is thought of as a MDOF system (Multiple-Degree-Of-Freedom system) having many modes of vibration. The resulting complicated FRF can be understood as a mathematical summation of SDOF FRF’s, each having a resonance frequency, damping factor, modal mass, modal stiffness and modal damping ratio.
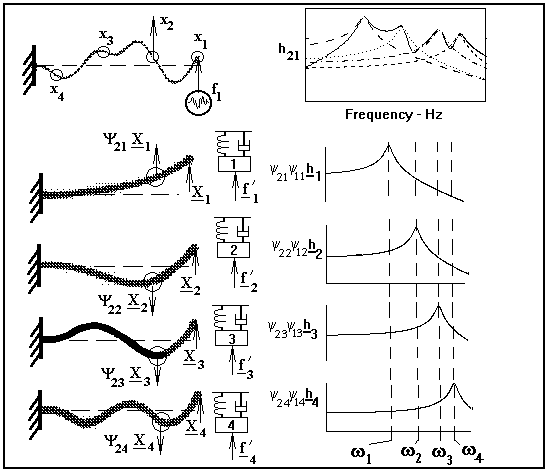
A complicated structure need not have distinct lumped masses and springs to be analyzed as a MDOF system. Product structural elements such as beams and panels represent MDOF components, given their many different modes of bending. Figure 4 summarizes the way in which products may be visualized as a superposition of SDOF modal components, even though lumped masses and springs are not involved. A cantelever beam serves as the example, exhibiting unique deformation patterns called mode shapes. The beam can be made to vibrate freely in any of the individual mode shapes, and again, associated with each mode shape is a resonance frequency, modal mass, modal stiffness, modal damping and a modal FRF.
Figure 4. A cantelever beam exhibits distinct vibration deformation patterns. Each deformation pattern, called a mode shape, behaves like a SDOF component. The measured FRF (upper right corner), X2/F1, is understood as a superposition of the SDOF FRF’s.
A useful thing to know about vibrating structures is that they can only vibrate using these unique mode shapes. Any arbitrary deformation produced in a vibration process (such as the upper left corner example of Figure 4 can only occur if it is comprised of the superposition of the natural mode shapes. This understanding, along with knowledge of the way in which the presence of specific vibrating mode shapes are manifest in measured data, arms one with valuable tools for establishing strategies for product defect detection.
Mode Shape Mathematics
A powerful mathematical concept presents mode shapes as a vehicle for transforming vector components like displacement, velocity, acceleration and force from their natural physical coordinate system to an abstract modal coordinate system. A matrix of mode coefficients, ψjr, represents all of the mode shapes of interest of a structure. The mode coefficient index, j, locates a numbered position on the structure (a mathematical degree of freedom) and the index, r, indicates the mode shape number. Modes are numbered in accordance with increasing resonance frequencies. The vector component coordinate transformation from abstract modal coordinates, X, to physical coordinates, X, is
{ X } = [ Ψ ]{ X } (6)
Each column in the [ Ψ ] matrix is a list of the mode coefficients describing a mode shape. Figure 4 shows the modal displacements, X1, X2, X3 and X4, defined at the end of the cantelever beam for each mode shape. As an example of the coordinate transformation, we see that the physical displacement at position number two, X2 (see Figure 2 upper left corner), is equal to the sum of the modal displacements weighted by the corresponding mode coefficients.
Now, any system having mass, stiffness and damping distributed throughout can be represented with matrices. Using such matrices a set of differential equations can be written for the Figure 2 cantelever beam, for example. The frequency domain form is
Displacements and forces at the numbered positions on the structure appear as elements in column matrices. The mass, damping and stiffness matrix terms are usually combined into a single dynamical matrix, [ D ]:
[ D ]{ X } = { F } (8)
A complete matrix, [ H ], of FRF’s would be the inverse of the dynamical matrix. Thus, we have the relationship,
{ X } = [ H ]{ F } (9)
Individual elements of the [ H ] matrix are designated with the notation, hjk(ω), where the j index refers to the row (location of response measurement) and the k index refers to the column (location of force). A column of the [ H ] matrix is obtained experimentally by applying a single force at a numbered point, k, on the structure while measuring the response motion at all n points on the structure, j = 1,2,3…n. The [ H ] matrix completely describes a structure dynamically. A one-time measurement of the [ H ] matrix defines the structure for all time… until a defect begins to develop. Then subtle changes crop up all over the [ H ] matrix. From linear algebra we have the transformation from the [ H ] matrix in modal coordinates to the physical [ H ] matrix.
This provides the understanding of a measured FRF, hjk(ω), as the superposition of modal FRF’s. Notice in the modal matrix [ H ] that the FRFs are uncoupled, i.e., modal FRFs appear only on the diagonal. This makes it easy to expand Equation (10) for any element of the physical [ H ] matrix (selecting out a row and column) to obtain the result:
Equation (11) is illustrated graphically in the upper right corner of Figure 2. The solid FRF curve, h21, is shown as an algebraic summation of the weighted modal FRF’s adjacent to each of the beam mode shapes in the figure. The resonance frequency of each mode of vibration depends on the effective modal mass and effective modal stiffness associated with each SDOF mode shape. The formula for modal resonances is the same as Equation (5):
 (12)
(12)
The modal damping fraction, ζr, depends on modal mass and modal stiffness because the critical damping value is a function of modal mass and modal stiffness:
(13)
Another useful FRF parameter is the phase angle, indicated by the real and imaginary parts of Equation (11). The phase angle function of frequency, θjk(ω), associated with hjk(ω) is:
Vibration theory seems overwhelming at times, but the multiplicity of modal parameters within a single FRF can now be appreciated as providing a rich source of indicators of product health.
Potential Failure Detection
One particularly attractive feature of dynamic defect detection using vibration measurements is the possibility of adjusting rejection criteria for identification of units having statistically significant potential for failure.
Mode shape definition, resonance frequency, and the modal damping factor are very sensitive to the mechanical condition of a product – so sensitive, in fact, that is not possible to manufacture two units with precisely identical FRFs. Slight differences between one unit and another will manifest themselves as deviations between their FRFs.
For example, a slightly loosened fastener can affect those mode shapes having large mode coefficients in the vicinity of the fastener. Notice in Equation (11) the effect of mode coefficients on the measured FRF. The loosened fastener will also affect modal stiffness in those modes, changing the resonance frequencies as set forth in Equation (12). Deviations in mode coefficients and resonance frequencies show up as shifts in FRF amplitude, locations of peaks, and phase angle. The damping factor, ζr, may be affected as a result of increased friction in loose joints. This shows up in the FRF as a broadening of peaks as ζr increases. Figure 5 overlays two FRFs that differ as a result of a slight change in just two of the structure modes. Two mode coefficients have been altered, along with a slight shift in the two resonance frequencies and damping factors.
While an exact theory underlying the relevance of vibration testing to failure potential is not fully developed, the concept is based on fatigue theory. It has been suggested that the fatigue life of certain components can be correlated with their damping factors and resonance frequencies. This would mean that the future operating life of some components could be estimated by measuring these modal parameters. On this basis limits could be established for rejecting units not expected to perform over a normal life span for the product.
Generally speaking, there are two broad defect detection strategies: theory based and phenomenological. The theory-based strategy attacks the problem with full knowledge of the product’s dynamic characteristics. The phenomenological strategy employs the same measurement and signal processing methods, but without knowledge of the system model. Both strategies provide the possibility of detecting the potential for premature failure.
Figure 1. Comparison of FRF’s for a baseline unit under test and a defective unit. Two modes have been affected by the defect, resulting in shifts in resonance frequencies, damping ratios and mode coefficients.
Theory-Based Defect Detection Strategies
The theory-based strategy includes experimental development of the global modal parameters, ωr, mr, kr and ζr along with the physical and modal FRF matrices, [ H ] and [ H ], and the mode shape matrix, [ Ψ ]. A standard process yielding this body of data is referred to as a modal test. The development of laboratories for performing modal tests is becoming more and more common in industry.
Also, Finite Element Modeling is often pressed into service as part of the strategy. Experimental modeling and analytical modeling provide a very effective approach when the two technologies are properly coordinated. The two methods are complimentary in many ways. Each has advantages and disadvantages when compared to the other.
Having an understanding of the modal characteristics of a product enables the development of multiple failure mode strategies. The mechanisms associated with different failure modes can be understood in relation to the various mode shapes and resonance frequencies of a product.
The theory-based strategy lends itself to strategically placed measurement devices (typically accelerometers or laser vibrometers). A quick glance at the mode shapes for the cantelever beam in Figure 4 indicates the end of the beam assures data that will involve every mode of the structure. An accelerometer positioned at a zero crossing for a particular mode shape will fail to produce any information about the health of that mode. The mode coefficient at that point would be zero and would remove that mode from the modal FRF summation as seen in Equation (11).
Assembly line vibration testing may involve an active operating product or a passive product. An operating electric motor provides its own vibration excitation. In this case the theory-based strategy provides an understanding of the modal forces generated by the motor. Having a modal model enhances the development of a test strategy.
A major pitfall in the implementation of the vibration defect detection method has to do with assembly line fixture design. Without an understanding of the way the unit under test is dynamically coupled to the fixture, the whole process could fail. Some plants have been found rejecting good units based on vibration measurements affected largely by fixture dynamics. This problem is easily avoided with a theory-based strategy in which all system characteristics, including fixture, are understood up front.
The analytical approach to defect detection requires special facilities and human resources. The technology is costly to implement and maintain in-house. Companies often prefer to rely on outside consultants to initiate the process and bring the assembly line into a routine production operation. Once the process is in place for a particular product, little specialization is required as long as the product is not subject to redesign.
Phenomenological Strategy
This strategy takes advantage of the dynamic characteristics of the product without really understanding the behavior. Dynamic measurement levels may be established across the frequency spectrum for an adequate statistical sample of good units. Then, out-of-tolerance levels are established as a basis for rejecting defective or potentially defective units. Plants engaging this strategy usually go through an extended period of tweaking failure criteria and limits before reaching a stable pass-fail process.